El arte no solamente está relegado a la capacidad artística del ser humano, sino que también se encuentra en la naturaleza de forma espontánea, formando complejas estructuras geométricas, de vivos colores, con patrones matemáticos. Este arte basado en las matemáticas y la geometría no solo lo encontramos a simple vista (nivel macroscópico) ya sea de cerca (flores, cristales de sal, conchas de caracol, etc.), o de lejos (formando estructuras de varios cientos de millones de años luz como las nebulosas y galaxias), sino que lo encontramos a nivel microscópico, y más aún a nivel atómico y subatómico. Vamos a ver un poco más como las matemáticas se esconden tras esas obras de arte de la naturaleza conocidas como las flores.

Diferentes formas de la naturaleza. Fotos de Wikimedia/Wikipedia.
De acuerdo con el registro fósil, el linaje de las plantas con flor (Angiospermas) surgió hace 150 millones de años (Ma), siendo el más reciente y el más abundante en especies de todos los linajes (>250.000 especies). Las plantas conquistaron el medio terrestre hace 450Ma (Embriofitas), radiándose en plantas no vasculares (briofitas) y vasculares (helechos, licofitas, gimnospermas, y angiospermas), hace 420Ma.
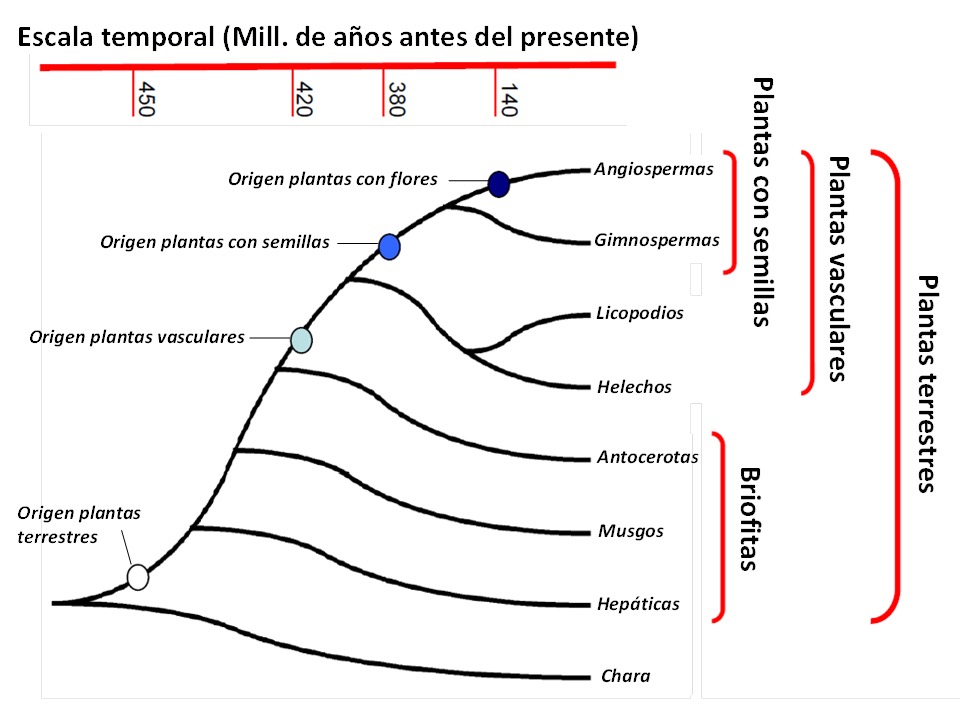
Esquema adaptado de Alvarez-Buylla et al. (2010).
La flor es la estructura más compleja de las plantas, y su función es reproductiva. La arquitectura floral básica se encuentra mayormente conservada entre las plantas conocidas como eucotiledóneas, que corresponden al 73% de las plantas con flores, conservando los diferentes elementos concéntricos de este órgano (desde afuera hacia adentro): sépalos (S), pétalos (P), estambres (órganos masculinos) y carpelos (órganos femeninos). Aunque las flores estén conservadas en eudicotiledóneas, existe una amplia variación en la simetría, forma, color y tamaño de las flores, número de involucros, número de órganos florales, etc. La mayor belleza reside en las pautas repetitivas de patrones de número y ciclo de sus involucros, creando auténticas obras de arte.

Passiflora caerulea (Wikimedia)
El estudio del desarrollo de la morfología de las plantas y sus órganos, basándose en patrones anatómicos, ha obsesionado a matemáticos y a botánicos desde hace muchos años. Empezando por el principio, las observaciones más antiguas de las que se conserva información, fue de los egipcios. Los patrones repetitivos ya se observaban con las hojas de acanto en los capiteles de las columnas de estilo Corintio, o los jeroglíficos con hojas de Lotus y hojas de Palmera datilífera. Teofrasto (370-285 a.C.) decía lo siguiente en una de sus obras respecto a una especie de planta: “aquellas que muestran hojas en series regulares”, desvelando este marcado carácter repetitivo y periódico en las plantas. De la misma forma hizo Plinio el viejo (23-79 d.C.) en su obra Historia Natural donde señalaba: “es una ramosa, planta pilosa con cinco o seis hojas en intervalos regulares, ubicadas en sentido circular alrededor de las ramas”. Leonardo Fibonacci de Pisa (1175-1240 d.C.) fue un matemático italiano que se dio cuenta de que en la naturaleza había ciertos patrones geométricos que seguían un patrón numérico repetitivo, que correlacionaba con la proporción aúrea. Por ejemplo, los capítulos florales del girasol (Helianthus annuus), presentan las semillas en 2 espirales, 34 de ellas en sentido de las agujas del reloj, y entre 21 y 55 en sentido antihorario. Por otro lado, hay dos tipos de piñas según el sentido de las brácteas. La división celular asimétrica de las células en los tejidos de las plantas nos ofrece una posible explicación para este tipo de estructuras en espiral, que se da tanto en hojas, como en tallos, flores, e inflorescencias.

Girasol. Fotos de Wikimedia/Wikipedia.
El matemático francés Benoît Mandelbrot descubrió en 1975 los fractales, cuyo término proviene del latín ‘fractus’ que significa ‘roto’ o ‘fracturado’, y al que él mismo se refería como “la geometría de la naturaleza”, y también “el arte de la rudeza” y “los elementos incontrolables de la vida”. Un fractal es un patrón geométrico natural que se autorreplica infinitamente, proyectando la figura completa a escalas pequeñas, para producir formas y texturas irregulares que escapan de los dominios de la geometría clásica. Los fractales se ven influenciados por dos factores: la forma y el ritmo. La planta típica para describir fractales en la naturaleza es el Romanescu, un tipo de brocoli con un aspecto muy llamativo, aunque también se encuentran estas estructuras fractales en numerosas especies de helechos y cactáceas, entre otras.

Varios ejemplos de fractales en plantas. Fotos de Wikimedia/Wikipedia.
Hay un grupo de investigación del Departamento de Ciencias Informáticas de la Universidad de Calgary (Alberta, Canadá), liderado por el Prof. Przemyslaw Prusinkiewicz, que estudia el modelado, simulación y visualización del desarrollo de las plantas. Tienen una herramienta de simulación llamada “Laboratorio Virtual” (Virtual Lab, ó V-Lab), y otra llamada L-studio, para analizar simulaciones basadas en la L-simetría de las fractales. Pueden descargarse estas aplicaciones en la página web del proyecto: http://algorithmicbotany.org/virtual_laboratory/
Lo cierto es que tras todas estas observaciones, entendemos que la naturaleza se emplea a fondo para crear arte, y que posee una paleta de recursos con infinitas posibilidades: la geometría, el ritmo (en ángulo, número y periodicidad), y los colores, los entremezcla para expresar en el lienzo de las plantas toda su belleza. El poeta británico Lord Byron lo resumió bien: <<El arte, la gloria, y la libertad se marchitan, pero la naturaleza siempre se mantiene bella>>.