El número áureo (también conocido con el nombre de proporción áurea o razón áurea) se define como aquel número algebraico irracional que surge de la división en dos de un segmento, guardando las siguientes proporciones: la longitud total a+b es al segmento más largo a, como a es el segmento más corto b. De esta manera, a menudo se le atribuye un carácter estético especial a los objetos cuyas proporciones se ajustan a este número, donde ya les adelanto que no son escasos los ejemplos que encontramos en la naturaleza. Poco a poco, a lo largo de este artículo, iremos desvelando algunos de ellos, aquellos que humildemente considero más interesantes.
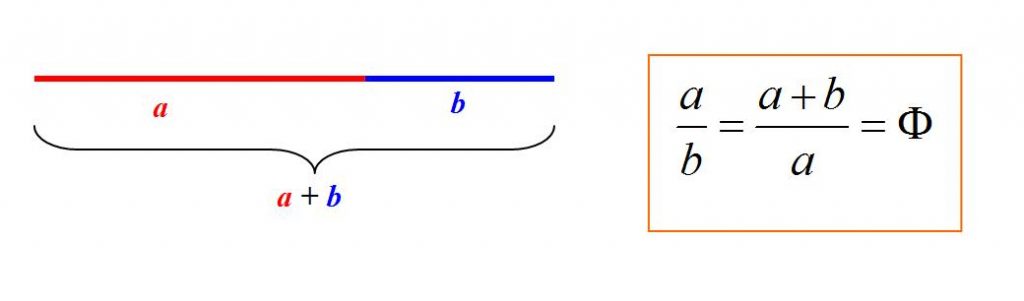
Se dice que dos segmentos están en proporción áurea (o en media y extrema razón) si se cumple la condición de que el total es al segmento mayor, como el segmento mayor es al segmento menor. ¿Han probado a llevar a cabo los cálculos?
El número áureo se deriva a partir de la sucesión de Fibonacci, la cual se inicia con 0 y 1, y a partir de éstos, cada nuevo elemento de la relación se define como el resultado de la suma de los dos elementos anteriores, siendo un ejemplo del mismo la siguiente progresión: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Esta serie fue descrita en Europa en el siglo XIII por el matemático italiano Leonardo de Pisa, conocido popularmente como Fibonacci (de ahí que esta serie matemática lleve el nombre de su descriptor o descubridor), con el fin de dar solución al siguiente problema sobre la cría de conejos:
“¿cuántos conejos (parejas de conejos) habrá en 12 meses si estos se reproducen continuamente y cada pareja de conejos produce una nueva pareja de conejos (un macho y una hembra) sabiendo que cada conejo se puede cruzar a la edad de un mes y siendo asimismo su período de gestación de un mes?”.
La solución al mismo, por si alguien quisiera consultarla, se recoge en el libro Liber Abaci, sin embargo, para no relatar los pormenores matemáticos de los que hizo uso el italiano, les pondré un ejemplo similar mucho más claro y conciso.
Los machos de una colmena de abejas tienen un árbol genealógico que cumple con la sucesión de Fibonacci a pies juntillas. Así, y a partir de un zángano (macho de la abeja), podemos trazar su genealogía. Para trazar el árbol genealógico del zángano (al que denotaremos con el término 1 de nuestra particular serie de Fibonacci) debemos tener en cuenta que éstos no tienen progenitores paternos, pero obviamente sí tienen tienen una progenitora materna (1, 1), dos abuelos (los padres de la abeja reina, es decir, 1, 1, 2 conforme subimos en el árbol genealógico de la colmena), tres bisabuelos (el padre de la reina no tiene padre, luego lo denotaríamos con las cifras 1, 1, 2, 3), cinco tatarabuelos (1, 1, 2, 3, 5), ocho trastatarabuelos (1, 1, 2, 3, 5, 8) y así sucesivamente con el resto de ascendentes familiares. Si alguien se atreve a dividir el número de hembras entre el número de machos de esta singular genealogía apícola apreciará que los resultados se aproximan con el paso de las generaciones a la razón áurea (cuyo valor es 1,618033).
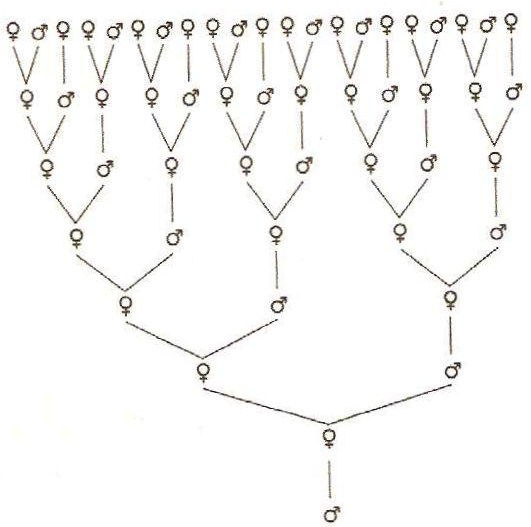
Si miramos la genealogía de una colmena cualquiera, observamos que los zánganos (abejas macho de una colmena) proceden de huevos sin fecundar (partenogenéticas). Por su parte, las hembras, que proceden de huevos fertilizados, tienen padres de ambos sexos.
Conforme ascendemos en el árbol genealógico, obtenemos los dígitos que conforman la sucesión de Fibonacci, de la cual se deduce la proporción áurea.
Bajo la proporción áurea, la naturaleza esconde bellas estampas, hasta el punto que casi resultaría imposible enumerarlas todas. Este es el motivo por el que he decidido centrar el resto del texto en aquellas proporciones áureas que se encuentran presentes o guardan relación con el cuerpo humano. Ya lo dijo el arquitecto e ingeniero romano Marco Vitruvio Polión:
“la Naturaleza ha diseñado el cuerpo humano de forma que sus miembros estén proporcionados a su estructura como un todo”.
En otras palabras, el romano consideraba el cuerpo humano un edificio perfecto. Así pues, y tomando como marco de trabajo la reflexión anterior, prepárense para una clase de matemáticas.
De hecho, el pensamiento de Marco Vitruvio Polión sigue muy vivo en la actualidad, puesto que no son pocos los atletas que dedican su vida por entero a la práctica del culturismo. Un ejemplo de lo anteriormente expuesto se puede ver en la modalidad denominada Women’s Physique, donde se premia la consecución de un cuerpo musculado y simétrico a la par que femenino. En definitiva, y aún sin ser conscientes de ello (imagino que no al menos en los términos matemáticos en los que pretendo transmitirlo yo), los jueces de este deporte lo que están premiando es la consecución de un cuerpo con razón o proporcionalidad áurea. Si no me creen, párense a mirar unos minutos la imagen de la atleta Eva Berenguer que se adjunta a este artículo.
La campeona del mundo de Bodyfitness por la IFBB (Federación Internacional de Fisicoculturismo y Fitness) en el año 2016 muestra un cociente cintura-cadera cercano a 0,8. Es decir, el contorno de su cintura es un poco inferior al de su cadera, tal y como se aprecia en la imagen. A este respecto, hay múltiples estudios antropológicos que justifican y argumentan la necesidad de acercarse a esta proporción, tal y como han establecido hasta la saciedad antropólogos como Marvin Harris. Más allá de otras disquisiciones, la razón principal es que esta proporción cintura-cadera nos resulta armoniosa, siendo este el motivo por el que los hombres, desde tiempos inmemoriales, encuentran más atractivas a las mujeres que cumplen estos estándares, puesto que una cadera con un perímetro un poco mayor que el de la cintura facilitaría la salida por el canal del parto del neonato. Los hombres somos tan primitivos, que nuestra armonía puede reducirse en términos de fecundidad. Por si esto fuera poco, supongamos por un instante que nuestra amiga Eva Berenguer se ajusta además fielmente a las medidas que se exigen a las denominadas “top model”, es decir, el clásico “90-60-90”, medidas que corresponden al contorno de pecho, cintura y cadera femenina respectivamente. Si procedemos a dividir el perímetro de la cadera entre el de la cintura… ¡el valor resultante es 1.5! ¡Un valor similar al de la razón áurea! Si se preguntan de dónde saqué el 0,8 con el que empezaba este párrafo, dividan 60 entre 90, (de acuerdo, el resultado es 0,67, no es 0,8). Es la inversa (o casi) de la proporción áurea.

Dividir distancia en media y extrema razón (proporción áurea) ha sido considerado desde tiempos inmemoriales sinónimo de belleza y armonía. Estas son dos de las muchas características que buscan los jueces en el cuerpo de una chica Bodyfitness, como el caso de la atleta barakaldesa Eva Berenguer.
[Imagen cortesía de Eva Berenguer].
Podríamos decir que es magia, pero su verdadero nombre es Matemáticas. Vamos a prescindir de nuestra amiga Eva Berenguer por unos instantes para que no me acusen de mentiroso o estar haciendo trampas. Fíjense en los dedos de sus manos y mida uno de ellos al azar, el que más le guste. Ahora, mida la falange más larga de cuantas componen ese dedo, que como ya sabrán, es la primera, es decir, la más cercana al metacarpo. En mi caso concreto, mi dedo índice derecho mide 9 centímetros en total, de los cuales, 5,3 corresponden a la primera falange. Dividan el primer entre el segundo. ¿El resultado? Como habrán averiguado ya, se acerca asombrosamente a phi. Les invito a que lo repitan tomando como referencia el dedo de su hijo, pareja, padre, madre o cualquier otra persona que tengan a su lado (siempre y cuando tengan su consentimiento previo). Algo similar ocurrirá al dividir la altura de su cabeza entre su anchura, o si lo prefieren, la altura de su pabellón auditivo entre su anchura. ¡Somo seres áureos! O al menos, tendentes a guardar esta proporción.
Los motivos por los que a nuestro cerebro le resultan especialmente estéticos todos aquellos objetos que guardan la proporción áurea se desconocen. Lo cierto y verdad es que los fabricantes de teléfonos móviles, televisiones de plasma o incluso cajetillas de tabaco son conscientes de que los objetos cuyas proporciones se acercan a la razón áurea nos resultan más atractivos, y de alguna manera, hay especialista en mercadotecnia que hasta se atreven a afirmar que lo hacen con el ánimo de hacernos consumir más ese determinado producto por el simple hecho de resultarnos atractivo. Quizás, nuestro gusto por los objetos que se ajustan a la proporción áurea sea un rasgo innato que se pierde en los albores de nuestro acervo genético. De hecho, tan arraigado está, que hasta el ADN es presa de él.
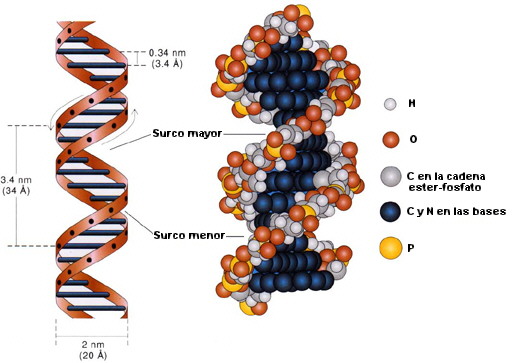
La proporción áurea está también presente en nuestro ADN, (fíjense en los surcos), motivo por el que quizás, los objetos que guardan esta proporción divina nos resultan tan atractivos, bellos y armoniosos.
El ADN (Ácido Desoxirribonucleico) es el material que contiene las instrucciones genéticas usadas en el desarrollo y funcionamiento de muchos organismos vivos y algunos virus. Se trata de una molécula bicatenaria, es decir, formada por dos cadenas dispuestas de manera antiparalela, presentando las bases nitrogenadas enfrentadas entre sí, conformando en conjunto una doble hélice de espiral dextrógira. Huelga decir que tal cantidad de información necesita enrollarse de manera eficiente y compacta, puesto que se debe tener libre acceso a los planos de “nuestro edificio” (conocido como cuerpo) sin que estos ocupen mucho espacio en nuestra mesa de trabajo cotidiana (a la que vamos a llamar célula). Para ello, las dos hebras de ADN se enrollan una sobre otra, de tal forma que para mantener enfrentadas entre sí las bases nitrogenadas (recuerden, siempre se enfrentan Guanina-Citosina y Adenina-Timina), cada par de bases debe girar con respecto a la anterior 36º. Esta especial forma de organización conlleva que se generen huecos o hendiduras en la molécula de ADN, más concretamente una hendidura mayor de 2,2 nanómetros de anchura y una menor de 1,2 nanómetros. En un último esfuerzo matemático, realicen la división: 2,2/1,2 = 1,83, o lo que es lo mismo, cercano a φ.
Como ya habrán podido advertir, nuestra vida cotidiana está plagada de proporciones matemáticas que en muchos casos ignoramos, probablemente porque quizás inconscientemente damos por hecho que no pueden ser de otra forma. Hay cosas que encontramos bellas o armoniosas y más allá de proporciones matemáticas, con eso nos basta. A este respecto, me gustaría dejar como despedida una reflexión que desde un tiempo a esta parte me vengo haciendo cada vez que escucho (no sin horrorizarme) ciertos comentarios. Me estoy refiriendo a aquellos que dan por hecho que una mujer, por el mero hecho de estar musculada, no puede ser femenina. También los hay que piensan que su desarrollada musculatura implica necesariamente que se trata de personas agresivas y violentas. Este tipo de opiniones creo que hablan mucho (y no precisamente bien) del tipo de sociedad que estamos formando en valores y educación. ¡A lo que ahora hay que añadir una total y absoluta falta de conocimientos matemáticos!


